Question

Jumping up before the elevator hits. After the cable snaps and the safety system fails, an elevator cab free-falls from a height of 36.0 m. During the collision at the bottom of the elevator shaft, a 85.0 kg passenger is stopped in 5.00 ms. (Assume that neither the passenger nor the cab rebounds.) What are the magnitudes of the (a) impulse and (b) average force on the passenger during the collision

Answer 1

a) I = -2257.6 Kg*m/s

b) F = -451,520N

Step-by-step explanation:

part a.

we know that:

I =
`P_f-P_i`

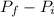
where I is the impulse,
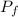`P_f` the final momentum and
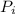`P_i` the initial momentum.

so:

I =
`MV_f-MV_i`

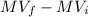
where M is the mass,
`V_f` the final velocity and
`V_i` the initial velocity.

Therefore, we have to find the initial velocity or the velocity of the passenger just before the collition.

now, we will use the law of the conservation of energy:

`E_i=E_f`

so:

mgh =
`(1)/(2)MV_i^2`

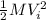
where g is the gravity and h the altitude. So, replacing values, we get:

(85kg)(9.8m/s^2)(36m)=
`(1)/(2)(85kg)V_i^2`

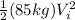
solving for
`V_i`:

`V_i = 26.56m/s`

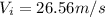
Then, replacing in the initial equation:

I =
`MV_f-MV_i`

I =
`(85kg)(0m/s)-(85kg)(26.56m/s)`

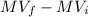
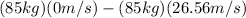
I = -2257.6 Kg*m/s

Then, the impulse is -2257.6 Kg*m/s, it is negative because it is upwards.

part b.

we know that:

Ft = I

where F is the average force, t is the time and I is the impulse. So, replacing values, we get:

F(0,005s) = -2257.6 Kg*m/s

solving for F:

F = -451520N

Finally, the force is -451,520N, it is negative because it is upwards.