Answer:
1.12191 m
Step-by-step explanation:
m = Mass of point = 2 kg
f = Frequency = 0.66 Hz
I = Moment of inertia = 1.28 kgm²
g = Acceleration due to gravity = 9.81 m/s²
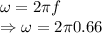
For a compound pendulum the angular velocity is given by
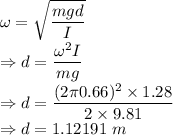
The distance of the pivot point from the center of mass of the object is 1.12191 m