Answer:
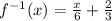
Explanation:
Given function.
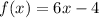
To find the inverse function

Step 1:
Replace
 with
with
 in the function.
in the function.
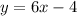
Step 2:
Interchange
 with
with
 in the equation.
in the equation.
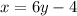
Step 3:
Solve for
 .
.
We have
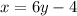
Adding 4 to both sides,
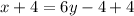
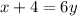
Dividing each term by 6 to isolate

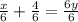
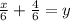
Simplifying fractions by dividing the numerator and denominator by their GCF.
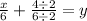
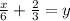
Thus the equation of
 is:
is:

Step 4:
Replace
 with
with

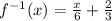 (Answer)
(Answer)
Thus, we have the inverse function