Question

What are the zeros of the polynomial function

F(x) = x^3-5x^2-6x

A. x= -2, x=0 and x=3
B. x=-1, x=0 and x=6
C. x=-3, x=0 and x=2
D. x=-6, x=0 and x=1

Answer 1

Option B

The zeros of the polynomial function are x = 0 , x = 6, x = -1

Solution:

Given function is:

`f(x) = x^3 -5x^2 - 6x`

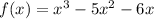
To find: zeros of the polynomial function

To find the zeros of polynomial function, set the function equal to zero and then solve for x.

`x^3 -5x^2 - 6x = 0`

Taking "x" as common term, we get

`x(x^2 - 5x - 6) = 0`

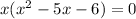
Equating to zero,

`x = 0 \text{ and } x^2 - 5x - 6 = 0`

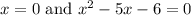
So one of the zeros of polynomial is x = 0

Let us solve
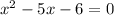`x^2 - 5x - 6 = 0` to find other zeros

Let us solve using quadratic formula,

`\text {For a quadratic equation } a x^(2)+b x+c=0, \text { where } a \\eq 0\\\\x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

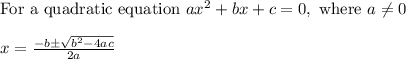
Using the above formula,

`\text{ for } x^2 - 5x - 6 = 0 \text{ we have } a = 1 ; b = -5 ; c = -6`

`\text{ The discriminant } b^2 - 4ac > 0 , \text{ so, there are two real roots }`

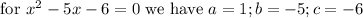
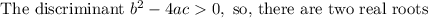
Substituting the values of a, b, c in above formula,

`x=\frac{-(-5) \pm \sqrt{(-5)^(2)-4(1)(-6)}}{2(1)}\\\\x=(5 \pm √(25+24))/(2)=(5 \pm √(49))/(2)\\\\x=(5 \pm 7)/(2)\\\\x=(5+7)/(2) \text{ or } x=(5-7)/(2)\\\\x=(12)/(2) \text{ or } x=(-2)/(2)\\\\x=6 \text{ or } x=-1`

Thus the zeros of the polynomial function are x = 0 , x = 6, x = -1