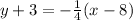Answer:
The required equation for the given point and the given slope is
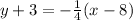
Explanation:
Given:
Let,
point A( x₁ , y₁) ≡ ( 8 ,-3)
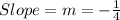
To Find:
Equation of Line Passing through A( x₁ , y₁) with slope = -1/4
Solution:
Equation of a line passing through a points A( x₁ , y₁) and having slope m is given by the formula,
i.e equation in point - slope form
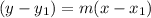
Now on substituting the slope and point A( x₁ , y₁) ≡ ( 8 ,-3) we get
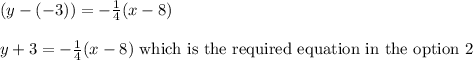
The required equation for the given point and the given slope is