Option C
The explicit formula for the arithmetic sequence is

Solution:
Given that the arithmetic sequence is:
3, -3, -9, -15, -21, ...
To find: Explicit formula for the arithmetic sequence
The nth term of an arithmetic sequence is given by:
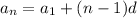
Where
 is nth term of sequence
is nth term of sequence
n is the term's location
 is the first term of sequence
is the first term of sequence
d is the common difference between terms
In an arithmetic sequence, the difference between successive terms is constant. This means that we can move from any term to the next one by adding a constant value.
In the given sequence:
3, -3, -9, -15, -21, ...
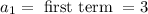
d = difference between any two terms in sequence
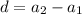
d = -3 - (3) = -6
Substituting the values in above formula,
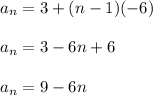
Thus the explicit formula to find any term in sequence is found