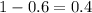Question

The time T that technician requires to perform preventive maintenance on an air conditioning unit has an unknown probability distribution. However, its mean is known to be 2 hours, with standard deviation 1 hour. Suppose the company maintains 70 of these units and that the conditions of the Central Limit Theorem apply. What is the probability that a maintenance operation will take more than 2 hours and 15 minutes?

Answer 1

0.4

Explanation:

To calculate the probability that a maintenance operation will take more than 2 hours and 15 minutes. We can first calculate the probability that ALL maintenance operation on 70 of the units will take less than 2 hours and 15 minutes, then subtract it from 1.

So the probability of a maintenance operation that would take less than 2 hours and 15 minutes, or 135 minutes is:

`P(X \leq 135, \mu = 120, \sigma = 60) = 0.6`

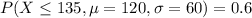
So the probability that a maintenance operation will take more than 2 hours and 15 minutes is:

`1 - 0.6 = 0.4`