Question

The Ostwald process is used commercially to produce nitric acid, which is, in turn, used in many modern chemical processes. In the first step of the Ostwald process, ammonia is reacted with oxygen gas to produce nitric oxide and water. What is the maximum mass of H 2 O H2O that can be produced by combining 52.3 g 52.3 g of each reactant? 4 NH 3 ( g ) + 5 O 2 ( g ) ⟶ 4 NO ( g ) + 6 H 2 O ( g )

Answer 1

35.3 g

Step-by-step explanation:

From the balanced equation given we can say:

4 moles of NH3 reacts with 5 moles of O2 to give 6 moles of H2O.

4*17 g of NH3 reacts with 5*32 g of O2 to give 6*18 g of H2O.

68 g of NH3 reacts with 160 g of O2 to give 108 g of H2O.

Here the limiting reagent is O2 and excess reagent is NH3.

52.3 g of O2 will react with
`(68)/(160)*52.3=22.23\ g\ of\ NH_(3)` to give :

`(108)/(160)*52.3=35.3\ g\ of\ H_(2)O`

Hence the maximum mass of H2O that can be produced by 52.3 g of reactants is 35.3 g.

Answer 2

35.3124 g is the maximum mass of
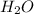`H_2O` that can be produced.

Step-by-step explanation:

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

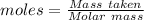
For
`NH_3` :-

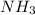Mass of
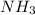`NH_3` = 52.3 g

Molar mass of
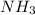`NH_3` = 17.031 g/mol

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

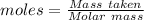
Thus,

`Moles= (52.3\ g)/(17.031\ g/mol)`

`Moles\ of\ NH_3= 3.0709\ mol`

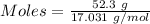
For
`O_2` :-

Given mass of
`O_2`= 52.3 g

Molar mass of
`O_2` = 31.9898 g/mol

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

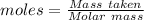
Thus,

`Moles= (52.3\ g)/(31.9898\ g/mol)`

`Moles\ of\ O_2=1.6349\ mol`

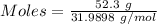
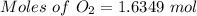
According to the given reaction:

`4NH_3+5O_2\rightarrow 4NO_4+6H_2O`

4 moles of
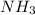`NH_3` reacts with 5 moles of
`O_2`

1 mole of
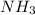`NH_3` reacts with 5/4 moles of
`O_2`

Also,

3.0709 moles of
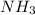`NH_3` reacts with
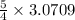`(5)/(4)* 3.0709` moles of
`O_2`

Moles of
`O_2` = 3.8386 moles

Available moles of
`O_2` = 1.6349 moles

Limiting reagent is the one which is present in small amount. Thus,
`O_2` is limiting reagent.

The formation of the product is governed by the limiting reagent. So,

5 moles of
`O_2` on reaction forms 6 moles of
`H_2O`

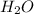
1 mole of
`O_2` on reaction forms 6/5 moles of
`H_2O`

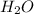
Thus,

1.6349 mole of
`O_2` on reaction forms
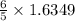`(6)/(5)* 1.6349` moles of
`H_2O`

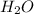
Moles of
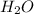`H_2O` = 1.9618 moles

Molar mass of
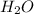`H_2O` = 18 g/mol

Mass of sodium sulfate = Moles × Molar mass = 1.9618 × 18 g = 35.3124 g

35.3124 g is the maximum mass of
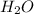`H_2O` that can be produced.