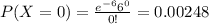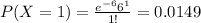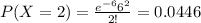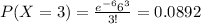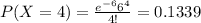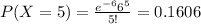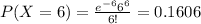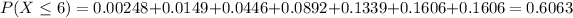Question

Suppose that the average number of airline crashes in a country is 2 per month. (a) What is the probability that there will be at least 3 accidents in the next month? Probability = 0.3233 (b) What is the probability that there will be at least 6 accidents in the next two months? Probability = 1-(643/(15e^4)) (c) What is the probability that there will be at most 6 accidents in the next three months? Probability =

Answer 1

a)
`P(X\geq 3)=1-P(X<3)=1-P(X\leq 1)=1-[0.1353+0.2707+0.2707]=0.3234`

b)
`P(X\geq 6)=1-P(X<6)=1-P(X\leq 5)=1-[0.0183+0.0733+0.1465+0.1954+0.1954+0.1563]=0.2148`

c)
`P(X\leq 6)=0.00248+0.0149+0.0446+0.0892+0.1339+0.1606+0.1606=0.6063`

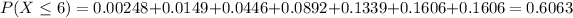
Explanation:

Let X the random variable that represent the number of airline crashes in a country. We know that
`X \sim Poisson(\lambda=2)`

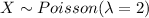
The probability mass function for the random variable is given by:

`f(x)=(e^(-\lambda) \lambda^x)/(x!) , x=0,1,2,3,4,...`

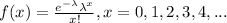
And f(x)=0 for other case.

For this distribution the expected value is the same parameter
`\lambda`

`E(X)=\mu =\lambda`

(a) What is the probability that there will be at least 3 accidents in the next month?

On this case we are interested on the probability of having at least three accidents in the next month, and using the complement rule we have this:

`P(X\geq 3)=1-P(X<3)=1-P(X\leq 1)=1-[P(X=0)+P(X=1)+P(X=2)]`

Using the pmf we can find the individual probabilities like this:

`P(X=0)=(e^(-2) 2^0)/(0!)=0.1353`

`P(X=1)=(e^(-2) 2^1)/(1!)=0.2707`

`P(X=2)=(e^(-2) 2^2)/(2!)=0.2707`

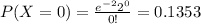
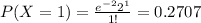
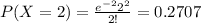
And replacing we have this:

`P(X\geq 3)=1-P(X<3)=1-P(X\leq 1)=1-[0.1353+0.2707+0.2707]=0.3234`

(b) What is the probability that there will be at least 6 accidents in the next two months?

For this case since we want the amount in the next two months the rate changes
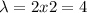`\lambda=2x2= 4` accidents per 2 months.

`P(X\geq 6)=1-P(X<6)=1-P(X\leq 5)=1-[P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)]`

Using the pmf we can find the individual probabilities like this:

`P(X=0)=(e^(-4) 4^0)/(0!)=0.0183`

`P(X=1)=(e^(-4) 4^1)/(1!)=0.0733`

`P(X=2)=(e^(-4) 4^2)/(2!)=0.1465`

`P(X=3)=(e^(-4) 4^3)/(3!)=0.1954`

`P(X=4)=(e^(-4) 4^4)/(4!)=0.1954`

`P(X=5)=(e^(-4) 4^5)/(5!)=0.1563`

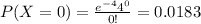
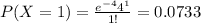
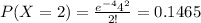
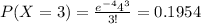
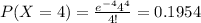
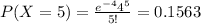
Replacing we got:

`P(X\geq 6)=1-P(X<6)=1-P(X\leq 5)=1-[0.0183+0.0733+0.1465+0.1954+0.1954+0.1563]=0.2148`

(c) What is the probability that there will be at most 6 accidents in the next three months?

For this case since we want the amount in the next two months the rate changes
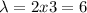`\lambda=2x3= 6` accidents per 3 months.

`P(X\leq 6)=P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)+P(X=6)`

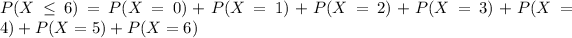
Using the pmf we can find the individual probabilities like this:

`P(X=0)=(e^(-6) 6^0)/(0!)=0.00248`

`P(X=1)=(e^(-6) 6^1)/(1!)=0.0149`

`P(X=2)=(e^(-6) 6^2)/(2!)=0.0446`

`P(X=3)=(e^(-6) 6^3)/(3!)=0.0892`

`P(X=4)=(e^(-6) 6^4)/(4!)=0.1339`

`P(X=5)=(e^(-6) 6^5)/(5!)=0.1606`

`P(X=6)=(e^(-6) 6^6)/(6!)=0.1606`

`P(X\leq 6)=0.00248+0.0149+0.0446+0.0892+0.1339+0.1606+0.1606=0.6063`