Question

Hey i need help with system of equations.
i uploaded an image

Answer 1

All proofs are given in the explanation

Explanation:

System Of Linear Equations

Given a system of equations of the form

`\displaystyle \left\{\begin{matrix}ax+by=c\\ dx+ey=f\end{matrix}\right.`

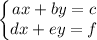
The solution of the systems is a pair of values x,y such that both conditions are met, i.e. the equations become identities.

We are given the following system

`\displaystyle \left\{\begin{matrix}x+y=7\\ 3x-2y=1\end{matrix}\right.`

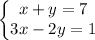
Part A. If we replace x=3, y=4 into both equations we get

`\displaystyle \left\{\begin{matrix}(3)+(4)=7\\ 3(3)-2(4)=1\end{matrix}\right.`

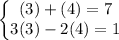
They are both now identities, so the solution is correct

Part B. If we multiply the first equation by 5 we get

`\displaystyle \left\{\begin{matrix}5x+5y=35\\ 3x-2y=1\end{matrix}\right.`

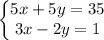
Adding both equations

`\displaystyle 8x+3y=36`

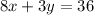
Part C. The new system will be

`\displaystyle \left\{\begin{matrix}x+y=7\\ 8x+3y=36\end{matrix}\right.`

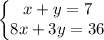
If we try again x=3, y=4 in the new system we get

`\displaystyle \left\{\begin{matrix}3+4=7\\ 8(3)+3(4)=36\end{matrix}\right.`

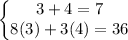
We can see both equations are now identities, so the solution holds also for this 'new' system

Part D. If we multiply or divide an equation by a constant, the conditions between the variables won't change, it's just another form to express the same relation. Adding two equations is exactly the same, it won't introduce any changes in the relationship between the variables, so the solution will always be the same