Question

5. Solve the following triangle for all missing sides and angles.

Part I: What is the measure of angle A?
Part II: Use the law of sines to find the length of side a.
Part III: Use the law of cosines to find the length of side b.
50 POINTS!! Please help. Make it simple, you can just give me the answer without explaining. PLEASE HELP!!!

Answer 1

`Part I: Measure of angle A=100°`

`Part II: Length of side a using sines law=29.56`

`Part III: Length of side a using sines law=24.21`

Explanation:

Given:-

`∠B = 45°`

`∠C = 35°`

`Length of side AB = 17`

Solution:-

1] To find Measure of ∠A=?

Solution:-

`Sum of angle of triangle = 180°`

`i.e. ∠A+∠B+∠C=180°`

`∠A+45+35=180`

`∠A=180-45-35`

`∠A=100°`

2] To find length of side a using sines law

Solution:-

`sines C = (opposite)/(hypotenuse)`

`sines C= (length AB)/(a)`

`sines C=(17)/(side a)`

`side a=(17)/(sines C)`

`side a=(17)/(0.575)`

`side a=29.56` ------------------------------ (equation 1)

3] To find length of side b using cosines law

Solution:-

`cosines C=(adjacent)/(hypotenuse)`

`cosines C=(lengthAC)/(hypotenuse)`

`cosines 35=(b)/(29.56)` ----------------------------(from equation )

`b=cosines 35\ times 29.56`

`b=0.819* 29.56`

`b=24.21`

Answer 2

Part I : 100°

Part II : a = 29.2

Part III : b = 20.95

Explanation:

See the attached diagram of the triangle.

Part I: ∠ A = 180° - ∠ B - ∠ C = 180° - 45° - 35° = 100°

Part II: Now, applying the law of sines, we have

`(AB)/(\sin 35^\circ) = (BC)/(\sin 100^\circ)`

⇒
`(17)/(\sin 35^\circ) = (a)/(\sin 100^\circ)`

⇒
`a = (17)/(\sin 35^\circ) * \sin 100^\circ`

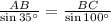
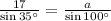
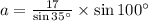
⇒ a = 29.2 (Answer)

Part III: Now, applying law of cosine, we have

b = a cos 35° + c cos 100° = 29.2 cos 35° + 17 cos 100° = 20.95 (Answer)