Question

2. At noon, ship A was 12 nautical miles due north of ship B. Ship A was sailing south at 12 knots (nautical miles per hour; a nautical mile is 2000 yards) and continued to do so all day. Ship B was sailing east at 9 knots and continued to do so all day. The visibility was 5 nautical miles. Did the ships ever sight each other?

Answer 1

No

Step-by-step explanation:

Let the reference origin be location of ship B in the beginning. We can then create the equation of motion for ship A and ship B in term of time t (hour):

A = 12 - 12t

B = 9t

Since the 2 ship motions are perpendicular with each other, we can calculate the distance between 2 ships in term of t

`d = √(A^2 + B^2) = √((12 - 12t)^2 + (9t)^2)`

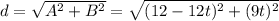
For the ships to sight each other, distance must be 5 or smaller

`d \leq 5`

`√((12 - 12t)^2 + (9t)^2) \leq 5`

`(12 - 12t)^2 + (9t)^2 \leq 25`

`144t^2 - 288t + 144 + 81t^2 - 25 \leq 0`

`225t^2 - 288t + 119 \leq 0`

`(15t)^2 - (2*15*9.6)t + 9.6^2 + 26.84 \leq 0`

`(15t^2 - 9.6)^2 + 26.84 \leq 0`

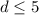
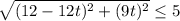
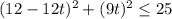
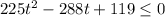
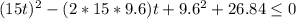
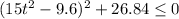
Since
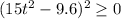`(15t^2 - 9.6)^2 \geq 0` then

`(15t^2 - 9.6)^2 + 26.84 > 0`

So our equation has no solution, the answer is no, the 2 ships never sight each other.