Question

A particular cylindrical bucket has a height of 36.0 cm, and the radius of its circular cross-section is 15 cm. The bucket is empty, aside from containing air. The bucket is then inverted so that its open end is down and, being careful not to lose any of the air trapped inside, the bucket is lowered below the surface of a fresh-water lake so the water-air interface in the bucket is 20.0 m below the surface of the lake.

To keep the calculations simple, use g = 10 m/s2, atmospheric pressure = 1. 105 Pa, and the density of water as 1000 kg/m3.a. If the temperature is the same at the surface of the lake and at a depth of 20.0 m below the surface, what is the height of the cylinder of air in the bucket when the bucket is at a depth of 20.0 m below the surface of the lake?b. If, instead, the temperature changes from 300 K at the surface of the lake to 275 K at a depth of 20.0 m below the surface of the lake, what is the height of the cylinder of air in the bucket?

Answer 1

12 cm

Step-by-step explanation:

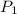`P_1` = Initial pressure =
`P_a=1* 10^5\ Pa`

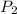`P_2` = Final pressure =
`P_a+\rho_w gh`

h = Depth of cylinder = 36 cm

g = Acceleration due to gravity = 10 m/s²

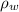`\rho_w` = Density of water = 1000 kg/m³

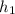`h_1` = Depth of lake = 20 m

From the ideal gas relation we have

`P_1V_1=P_2V_2\\\Rightarrow P_a(\pi r^2h)=(P_a+\rho_w gh_1)\pi r^2h'\\\Rightarrow 1* 10^5* 36=(1* 10^5+1000* 10* 20)h'\\\Rightarrow h'=(1* 10^5* 36)/(1* 10^5+1000* 10* 20)\\\Rightarrow h'=12\ cm`

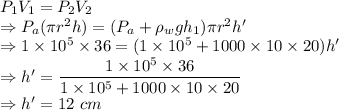
The height of the cylinder of air in the bucket when the bucket is at the given depth is 12 cm