Answer:
a) r₁ = 3.836 10⁷ m, b) F = - 3,390 10⁸ N , c) R = 120.3 m
Step-by-step explanation:
a) This is a problem of equilibrium where the force is gravitational, we call F1 the force of the Moon and F2 the force from the earth.
F₁ -F₂ = 0
F₁ = F₂
G m
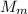 / r₁² = G m
/ r₁² = G m
 / r₂²
/ r₂²
Let's look for the measured distance from a Coordinate System located on the Moon,
r₂ = D - r₁
Where D is the average distance from Terra to the Moon 3.84 10⁸ m
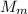 / r₁² =
/ r₁² =
 / (D - r₁)²
/ (D - r₁)²
(D² - 2 D r₁ + r₁²) =
 /
/
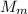 r₁²
r₁²
(1 -
 /
/
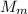 )r₁² - 2D r₁ + D² = 0
)r₁² - 2D r₁ + D² = 0
Let's replace and solve the second degree equation
(1 - 5.98 10²⁴ / 7.36 10²²) r₁² - 2 3.84 10⁸ r₁ + (3.84 10⁸)² = 0
-80.25 r₁² - 7.68 10⁸ r₁ + 14.75 10¹⁶ = 0
r₁² + 9.57 10⁶ r₁ - 1.838 10¹⁵ = 0
r₁ = [-9.57 10⁶ ±√ (91.58 10¹² + 7.352 10¹⁵)] / 2
r₁ = [-9.57 10⁶ + - 86.28 10⁶] / 2
The results are:
r₁’= 38.355 10 6 m
r₁ ’’ = -47.915 10 6 m
We take the positive result that a distance between the moon and the Earth, the equalization point is r₁ = 3.836 10⁷ m
b) The force at point R = 2 r₁
R = 2 3.8355 10⁷ = 7.671 10⁷ m
F = F₁ - F₂
F = G m
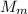 / R² - G m
/ R² - G m
 / (D- R)²
/ (D- R)²
F = G m (
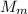 / R² -
/ R² -
 / (D-R)²)
/ (D-R)²)
F = m 6.67 10⁻¹¹ (7.36 10²² / (7.671 10⁷)² - 5.98 10²⁴ / (3.84 10⁸ - 0.7671 10⁸)²
F = m 6.67 10⁻¹¹ (0.125076 10⁸ - 0.63329 10⁸)
F = m (-3.3897 10⁸) N
The mass m of the rocket must be known, suppose it is worth 1 kg (m = 1 kg)
F = - 3,390 10⁸ N
c) let's use gravitational force from the moon
F = G m
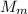 / R²
/ R²
R =√ G m
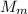 / F
/ F
R = √ (6.67 10⁻¹¹ 1 7.36 10²² / 3.3897 10⁸)
R = √ (1.4482 10⁴)
R = 1.2034 10² m
R = 120.3 m