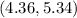Question

Assume that the helium porosity (in percentage) of coal samples taken from any particular seam is normally distributed with true standard deviation 0.76.(a) Compute a 99% CI for the true average porosity of a certain seam if the average porosity for 16 specimens from the seam was 4.85. (Give answers accurate to 2 decimal places.)

Answer 1

Answer:
`(4.36, 5.34)`

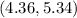
Explanation:

Formula to calculate the confidence interval for population mean is given by :-

`\overline{x}\pm z^*(\sigma)/(√(n))`

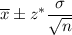
, where
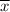`\overline{x}` = sample mean

n= sample size.

z*= Critical value

`\sigma` = Population standard deviation.

As per given , we have

`\sigma=0.76`

`\overline{x}=4.85`

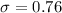
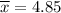
n= 16

From z-table , the critical value for 99% confidence = z*=2.576

Now , 99% confidence interval for true average porosity of a certain seam will be :

`4.85\pm (2.576)(0.76)/(√(16))`

`4.85\pm (2.576)(0.76)/(4)`

`4.85\pm (2.576)(0.19)`

`4.85\pm (0.48944)`

`=(4.85-0.48944\ 4.85+0.48944) \\\\=(4.36056,\ 5.33944)\approx(4.36,\ 5.34)`

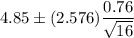
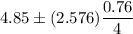
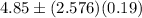
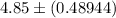
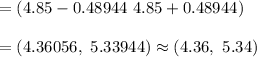
Hence, the required 99% CI for the true average porosity of a certain seam =
`(4.36, 5.34)`