Question

Help! How do you explain that √(m+n)=√m+ √n is not true for all values? (Example: m=5 and n=4)

Answer 1

Square the expressions to see the difference.

Explanation:

`$ √((m + n)) $`.

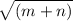Squaring this we have:
`$ (√(m + n))^2 = m + n $`

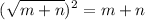
Now,
`$ √(m) + √(n) $`

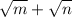
Squaring this we get:
`$ (√(m))^2 + (√(n))^2 = m + n + 2 √(mn) $`

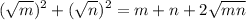
For the two expressions to be equal, we should have

`$ m + n = m + n +2√(mn) $` ⇔
`$ √(mn) = 0 $`.

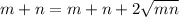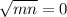This is possible iff mn = 0. i.e, m = 0 or n = 0.

Otherwise, they are not equal.

When m = 5 and n = 4.

`$ √(5 + 4) = √(9) = 3 $`

`$ √(5) + √(4) = √(5) + 2 $`

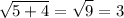
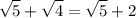
First is an integer. Second is an irrational number.

Clearly, they are not equal.