Question

In a measurement of a man’s density he is found to have a mass of 75.0 kg in air and an apparent mass of 2.25 kg when completely submerged in water with his lungs empty. He has a lung capacity of two and half liters. (a) What mass of water does he displace? (b) Determine his volume. (c) Calculate his density. (d) If his lungs are half filled with air, will he float or sink? (Show calculation. Yes/No without calculations give you zero points.) (e) If his lungs are completely filled with air, will he float or sink?

Answer 1

a)
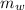`m_(w)` = 72.75 kg , b) V = 0.07275 m³ , c) ρ₂ = 1030.9 km / m³ , d) ρ₂= 996 kg / m³ float

Step-by-step explanation:

This is an exercise that we must solve using the Archimedes principle, where the thrust is

B = ρ g V

a) Let's use Newton's second law

F = B - W

F = ρ g V - mg

The force is the apparent weight (m₂ = 2.25 kg) is directed downwards so it is negative

F = m₂ g

-m₂ g = ρ g V - m g

-m₂ g =
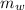`m_(w)` g - mg

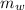`m_(w)` = -m₂ + m

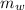`m_(w)` = -2.25 + 75.0

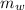`m_(w)` = 72.75 kg

b) let's use the definition of density

ρ = m / V

V = m /ρ

V = 72.75 / 1000

V = 0.07275 m³

c) the density of man is

ρ₂ = m / V

ρ₂ = 75.0 / 0.07275

ρ₂ = 1030.9 km / m³

d) the volume of man increases because the lungs are full of air, as they are half full, with a capacity of 2.5 liters and two lungs the volume is

V’= ½ 2.5 2

V’= 2.5 liters

V’= 2.5 10⁻³ m³

The total volume of man is

Vt = 0.07275 + 0.0025

Vt = 0.07525

Let's calculate the density

ρ₂ = 75.0 / 0.07525

ρ₂= 996 kg / m³

As this is less than the density of water (1000 kg / m3) man must float