Question

The pH of a solution is the negative logarithm of the molar concentration of hydronium ion, that is, pH=−log[H3O+] In neutral solutions at 25 ∘C, [H3O+]=10−7 M and pH=7. As [H3O+] increases, pH decreases, so acidic solutions have a pH of less than 7. Basic solutions have a pH greater than 7. The hydroxide and hydronium ion concentrations are related by the the ion-product constant of water, Kw , as follows: Kw=1.0×10−14=[H3O+][OH−] In the same way as the pH, we can define the pOH as pOH=−log[OH−]. It follows from the Kw expression that pH+pOH=14.

Answer 1

1.
`pH = -log[H^+]`

2. Acidic: pH < 7.00, neutral: pH = 7.00, basic: pH > 7.00

3. pH + pOH = 14.00 at room temperature

Step-by-step explanation:

Firstly, it is true that pH is defined as the negative logarithm of the concentration of hydronium ions. A simple rule for any p-function in chemistry is to remember that p = -log. For example:

`pH = -log[H^+], pK_a = -log(K_a)` etc.

Secondly, neutral solutions are the ones which have equal concentrations of hydronium and hydroxide ions regardless of the temperature. At room temperature, specifically, for pure solutions:

`[H_3O^+] = [OH^-] = 1.00\cdot 10^(-7) M`

Notice that applying the equation above:

`pH = -log[H_3O^+] = -log(1.00\cdot 10^(-7)) = 7.00`

This means neutral solutions at room temperature have a pH value of 7.00.

Now, let's say the concentration of hydronium increases to a value of:

`[H_3O^+] =2.00\cdot 10^(-7) M`

Then:

`pH = -log[H_3O^+] = -log(2.00\cdot 10^(-7)) = 6.70`

Notice that an increase in the molarity of hydronium lead to a decrease in pH. Therefore, acidic solutions have a pH < 7.00, while basic solutions have a pH > 7.00. Neutral solution was described as the one having pH = 7.00.

Thirdly, ion-product constant of water is defined as:

`K_w=[H_3O^+][OH^-]`

The given value of:

`K_w=[H_3O^+][OH^-]=1.00\cdot10^(-14)`

Is only valid at room conditions. Now let's take the -log of both sides:

`-log(K_w)=-log([H_3O^+][OH^-])`

Apply the rule of logs:

`-log(a\cdot b) = -log (a) + (-log (b)) = pa + pb`

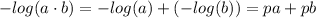
We obtain:

`pK_w = pH + pOH = -log(1.00\cdot 10^(-14)) = 14`

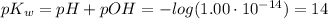
That said, the equation is proved.