Question

ulissa is running a 10-kilometer race at a constant pace. After running for 18 minutes, she completes 2 kilometers. After running for 54 minutes, she completes 6 kilometers. Her trainer writes an equation letting t, the time in minutes, represent the independent variable and k, the number of kilometers, represent the dependent variable. Which equation can be used to represent k, the number of kilometers Julissa runs in t minutes? k – 2 = k minus 2 equals StartFraction 1 Over 9 left-parenthesis t minus 18 right-parenthesis.(t – 18) k – 18 = k minus 18 equals StartFraction 1 Over 9 left-parenthesis t minus 2 right-parenthesis.(t – 2) k – 2 = 9(t – 18) k – 18 = 9(t – 2)

Answer 1

k – 2 = (t – 18) this is the answer

Answer 2

`\displaystyle k - 2 = (1)/(9)\, (t -2 )`.

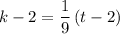Explanation:

Note that Ulissa is running at a constant pace. This problem is very similar to finding the equation for a line on an
`x`-
`y` plane given two points on that line. In this case, time
`t` (in minutes) acts as the dependent variable and acts as,
`x`. Distance
`k` acts as the dependent variable,
`y`.

Start by finding the slope of that line: given two points on that line
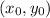`\left(x_0, y_0\right)` and
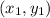`\left(x_1, y_1\right)`, the slope of that line would be equal to

`\displaystyle (y_1 - y_0)/(x_1 - x_0)`.

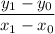In this case, the variables are different but the formula shall still apply. Note that the dependent variable
`k` is on the numerator while the independent variable
`t` is on the denominator. Apply the formula to find slope:

`\displaystyle (6 - 2)/(54 - 18) = (1)/(9)`.

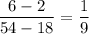Apply the slope-point form to any point on the line to obtain the line's equation. Note that this problem provided two points. They will produce two equivalent equations.

The slope-point form of a line with slope
`m` and a point
`(x_0, y_0)` will be:

`y - y_0 = m \, \left(x - x_0\right)`.

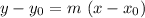In this question, applying the formula to the point
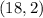`(18, 2)` will give the equation:

`\displaystyle k - 2 = (1)/(9)\, (t - 18)`.

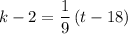Similarly, applying the formula to the point
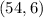`(54, 6)` will give the equation:

`\displaystyle k - 6 = (1)/(9)\, (t - 54)`.