Question

A local politician, running for reelection, claims that the mean prison time for car thieves is less than the required 4 years. A sample of 80 convicted car thieves was randomly selected, and the mean length of prison time was found to be 3 years and 6 months, with a population standard deviation of 1 year and 3 months.

Using a 3% level of significance, test the politician's claim.(a) State the null and alternative hypotheses for the test and calculate the value of the test statistic for this test.(b) Determine the critical region(s) for this test and state the conclusion of this test. Give a reason for your answer

Answer 1

There is significant evidence that mean prison time for car thieves is less than the required 4 years.

Explanation:

let mu be the mean prison time for car thieves

`H_(0)`: mu=4 years

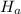`H_(a)`: mu<4 years

Test statistic can be calculated using the equation

z=
`(X-M)/((s)/(√(N) ) )` where

• X sample mean prison time for car thieves (3.5 years)

• M is the required prison time for car thieves (4 years)

• s is the standard deviation (1.25 years)

• N is the sample size (80)

z=
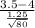`(3.5-4)/((1.25)/(√(80) ) )` ≈ -3.58

critical vale for the 3% level of significance is -1.88.

Since -3.58<-1.88, we can reject the null hypothesis.

There is significant evidence that mean prison time for car thieves is less than the required 4 years.

This is because the probability that the sample is drawn from the population where mean prison time for car thieves is 4 years is less than 3%.