Question

A conical tent has a radius of 10.4 ft and a height of 8.4 ft. Doubling which dimensions will quadruple the volume of the tent?

Answer 1

Answer: Doubling the radius.

Explanation:

The volume of a cone can be found with the following formula:

`V=(1)/(3)\pi r^2h`

Where "r" is the radius and "h" is the height of the cone.

Let's find the volume of the conical tent with a radius of 10.4 feet and a height of 8.4 feet.

Identifiying that:

`r=10.4\ ft\\\\h=8.4\ ft`

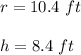
You get this volume:

`V_1=(1)/(3)\pi (10.4\ ft)^2(8.4\ ft)\\\\V_1=951.43\ ft^3`

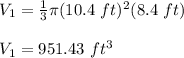
If you double the radius, the volume of the conical tent will be:

`V_2=(1)/(3)\pi (2*10.4\ ft)^2(8.4\ ft)\\\\V_2=3,805.70\ ft^3`

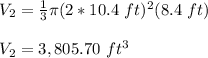
When you divide both volumes, you get:

`(3,805.70\ ft^3)/(951.43\ ft^3)=4`

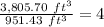
Therefore, doubling the radius will quadruple the volume of the tent.