Question

Assume the heights of women in a population follow the normal distribution with mean 64.3 and standard deviation 2.6 in.

a. A woman is randomly selected from the population.Calculate the probability that the height for the woman is:

i. Between 60 and 66 inches tall.

ii. Over 67 inches tall

b. How tall is a woman whose height is at the 90th percentile?

c. What is the median height of women?

d. A certain woman has a height that is 0.5 standard deviations above the mean. What proportion of women are taller than she?

e. What height separates the smallest 10% of heights from the largest 90%?

f. Five women are chosen at random from this population. What is the probability exactly one of them is more than 67 inches tall?

Answer 1

Explanation:

given that the heights of women in a population follow the normal distribution with mean 64.3 and standard deviation 2.6 in.

Let X be the height of the woman

a)

i)
`P(60<x<66) \\=0.7434- 0.0491\\=0.6943`

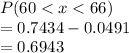
ii)
`P(X>67) = 1-0.8505\\\\=0.1495`

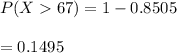
b) 90th percentile is 67.628

(Mean + 1.28 times std deviation)

c) Median = mean sinc enormal distribution

Median = 64.3 inches

d) P(Z>0.5) =
`1-0.6915\\=0.3085`

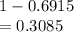
e) 10th percentile =60.972

Difference between 90th and 10th percentile

=
`67.628-60.972\\=6.656`

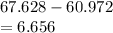
e) Each women is independent of the other.

For any woman to be taller than 67 inches is 0.1495 is constant for each women

So Y no of women taller than 67 is binomial with n =5

P(Y=1)= 0.3911