Answer:
s(t)=7t
Step-by-step explanation:
We are given that
Length of side of square initially=0 cm
Side of square increasing at the rate=
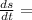 7 cm/s
7 cm/s
We have to find the formula to express the side length of the square s(in cm) in terms of the number of seconds t.
According to question
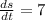
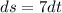
Taking integration on both sides then, we get
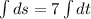

Substitute t=0 and s=0
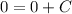
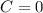
Now, substitute the value of C then, we get
s(t)=7t
This is required formula that express the side length of the square s(in cm) in terms of the number of seconds t, since the square's side length began growing.