Answer:
She must wash at least 13 cars
Explanation:
let:

Now, mathematically we can define:
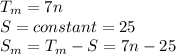
Where:
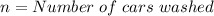
Now, we need to express the situation as a inequality. In this case, she wants to have at least $65 in spending money, so the inequality can be written as:
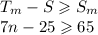
Solving for n:
add 25 to both sides:
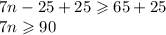
divide both sides by 7:
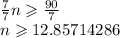
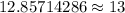
Therefore, Grace must wash at least 13 cars in order to have $65 in spending money