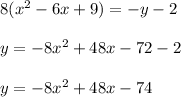Question

A parabola that has a vertex of (3, -2) a focus of (3, -2 1/16) , and opens downward. Which of the following best represents the equation of the parabola in standard form?

Answer 1

y = –x2 + 6x – 11

Explanation:

plz give brailyest and this one is the actual answer

Answer 2

`y=-8x^2+48x-74`

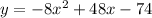
Explanation:

A parabola that has a vertex of (3, -2) a focus of (3, -2 1/16), then the line of symmetry is x = 3.

The distance between the vertex and focus is equal to p/2, so

`(p)/(2)=\sqrt{(3-3)^2+\left(-2+2 (1)/(16)\right)^2}=(1)/(16),`

so parabola's equation in vertex form is

`(x-x_0)^2=-2p(y-y_0)\\ \\(x-3)^2=-2\cdot (1)/(16)\cdot (y+2)\\ \\(x-3)^2=-(1)/(8)(y+2)\\ \\8(x-3)^2=-(y+2)`

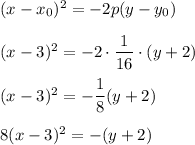
In standard form this equation is

`8(x^2-6x+9)=-y-2\\ \\y=-8x^2+48x-72-2\\ \\y=-8x^2+48x-74`