Question

Three hundred people buy raffle tickets. Three winning tickets will be drawn at random.

a. If first prize is $4000, second prize is $3500, and third prize is $400, in how many different ways can the prizes be awarded?
b. If each prize is $3500, in how many different ways can the prizes be awarded?

Answer 1

a) The first, second and third prizes can be awarded in 6 ways

b) The $3500 prize can be awarded in 1 way.

Explanation:

All the questions (a and b) are permutation question. And Permutation tries to tell us in how many ways we can arrange an object

a) The first part of the question requires us to to find the different ways in which first prize, second prize and third prize can be awarded. We have three object here. Using permutation formula which is n!; we have:

`3! = 3 * 2 * 1\\= 6 ways`

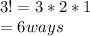
The prizes can be awarded in 6 ways. The ways can be described:

$4000, $3500, $400

$4000, $400, $3500

$3500, $400, $4000

$3500, $4000, $400

$400, $3500, $4000

$400, $4000, $3500

b) For the second part; the prize is $3500 which is a single instance and identical if replicated. So, the prize of $3500 can be awarded in 1 way only.