Question

The ratio of the area to the circumference of a circle is 5/4. What is the circumference of the circle?

Answer 1

The circumference of the circle is 16.

Explanation:

Given:

The ratio of the area to the circumference of a circle is 5/4.

Now, to find the circumference of the circle.

So, we get radius(r) first to find circumference.

For, getting radius(r) we use the proportion:

`(Area)/(circumference) =(5)/(4)`

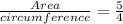
Now, putting formula to solve it:

⇒
`(\pi r^2)/(2\pi r) =(5)/(4)`

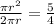
On solving we get:

⇒
`(r)/(2)=(5)/(4)`

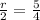
By multiplying with 2 on both sides we get:

⇒
`r=(5)/(4) * 2`

⇒
`r=(10)/(4)`

⇒
`r=2.5.`

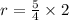
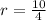
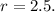
Radius = 2.5.

Now, putting the formula to get the circumference:

`Circumference = 2\pi r`

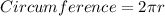
Taking the value of π = 3.14.

`Circumference = 2* 3.14* 2.5`

`Circumference = 15.7`

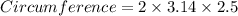
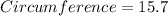
Circumference = 16 (approximately).

Therefore, the circumference of the circle is 16.