Question

A candy man manufacture wishes to mix two candies as a sales promotion when candy sells for $3per pound in other cells for $1.75 per pound the manufacture which is to have 1000 lbs of a mixture and stir the mixture for $2.35 per lbs how many pounds of each candy should be used in the mixture

Answer 1

`\displaystyle x=480\ ,\ y=520`

Explanation:

System Of Two Linear Equations

A system of two linear equations is given as

`\displaystyle \left\{\begin{matrix}ax+by=c\\ dx+ey=f\end{matrix}\right.`

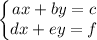
We must find the values of x and y who make both equations comply, i.e. they become identities

The question talks about one candy who sells for $3 per pound and others who sells for $1.75 per pound. Let's call x and y the pounds of each candy that must be used in a mixture with the conditions that:

• 1000 lbs of the mixture will be produced
• They will be sold for $2.35 per lb, i.e. for a total of $2,350

We form the system with both conditions

`\displaystyle \left\{\begin{matrix}x+y=1000\\ 3x+1,75y=2,350\end{matrix}\right.`

Multiplying the second equation by 4

`\displaystyle \left\{\begin{matrix}x+y=1,000\\ 12x+7y=9,400\end{matrix}\right.`

Multiplying the first equation by -7

`\displaystyle \left\{\begin{matrix}-7x-7y=-7,000\\ 12x+7y=9,400\end{matrix}\right.`

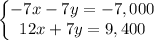
Adding both equations

`\displaystyle 5x=2,400`

`\displaystyle x=480`

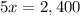
Using the relation

`\displaystyle x+y=1,000`

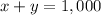
We solve for y

`\displaystyle y=1,000-480`

`\displaystyle y=520`

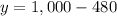
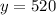
The solution is

`\displaystyle x=480\ ,\ y=520`