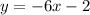Question

Write an equation of the line passing through the given points.
(1.-8) and (-2.10)
y=?​

Answer 1

The equation of line is
`y=-6x-2`

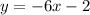
Explanation:

Given:

A line with two points on it are (1, -8) and (-2, 10)

Now, slope of a line passing through two points
`(x_1,y_1)\ and\ (x_2,y_2)` is given as:

`m=(y_2-y_1)/(x_2-x_1)`

Plug in
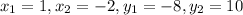`x_1=1,x_2=-2,y_1=-8,y_2=10` in the above and solve for 'm'. This gives,

`m=(10-(-8))/(-2-1)\\\\m=(10+8)/(-3)\\\\m=(18)/(-3)=-6`

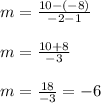
Now, the equation of a line with slope 'm' and a point on it as
`(x_1,y_1)` is given as:

`y-y_1=m(x-x_1)`

Plug in -6 for 'm',
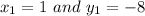`x_1=1\ and\ y_1=-8`. This gives,

`y-(-8)=-6(x-1)\\y+8=-6x+6\\y=-6x+6-8\\y=-6x-2`

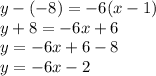
Therefore, the equation of a line passing through the given points (1, -8) and (-2, 10) is
`y=-6x-2`