Answer:

Explanation:
Given:
The quadratic equation in vertex form is given as:
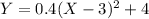
The standard form of a quadratic equation is:
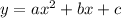
Now, in order to convert the given equation into standard form, we have to expand
 using the binomial expansion given by:
using the binomial expansion given by:
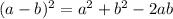
Here,
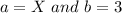
Therefore,
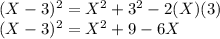
Now, plug in this expanded form into the original equation. This gives,
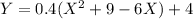
Now, we use distribute 0.4 inside the parenthesis. This gives,
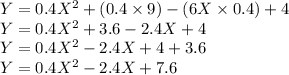
Therefore, the standard form of the given equation is:
