Answer:
CD = 6.52 cm
Explanation:
It is given that the cone is right angled cone with, a slant height of 16 cm, and a radius of 7 cm.
By, pythagoras theorm,
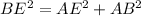
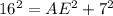
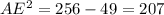
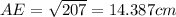
Thus, EC = 14.387 - 1 = 13.387 cm,
It can be seen that triangles ABE and CDE are similar.
Thus,
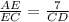
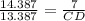
CD = 6.513 cm ≈ 6.52 cm