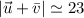Question

A vector u has a magnitude of 15 and a direction of 0 degrees. A vector v has a magnitude of 9 and a direction of 35 degrees. Find the direction and magnitude of u+v to the nearest whole values

Answer 1

`\displaystyle \alpha \simeq 13^o`

`\displaystyle \left | \vec{u}+\bar{v} \right |\simeq 23`

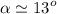
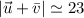
Explanation:

Sum Of Vectors

Given

`\displaystyle \vec{u}=<a,b>, \vec{v}=<c,d>`

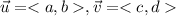
the sum of both is

`\displaystyle \vec{u}+\vec{u}=<a+c,b+d>`

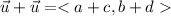
Given a vector

`\displaystyle \vec{x}=<m,n>`

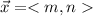
The magnitude of \vec x is

`\displaystyle \left | \vec{x} \right |=√(m^2+n^2)`

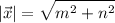
And the angle is forms with the positive x-axis is

`\displaystyle tan\alpha =(n)/(m)`

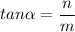
We have

`\displaystyle \vec{u}=<15\ cos0^o,15\ sin\ 0^o>`

`\displaystyle \vec{u}=<15,0>`

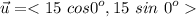
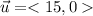
Also

`\displaystyle \vec{v}=<9\ Cos\ 35^o,9\ sin\ 35^o>`

`\displaystyle \vec{v}=< 7.372,5.162>`

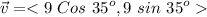
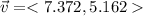
The sum of both vectors is

`\displaystyle \vec{u}+\vec{v}=<15+7.372,0+5.162>`

`\displaystyle \vec{u}+\vec{v}=<22.732,0+5.162>`

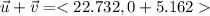
The magnitude of the sum is

`\displaystyle \left | \vec{u}+\vec{v} \right |=√(22.732^2+5.162^2)=22.96`

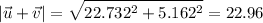
We compute the angle (direction)

`\displaystyle tan\alpha =(5.162)/(22.732)=0.227`

`\displaystyle \alpha =12.79^o`

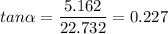
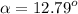
Rounding to the nearest integer

`\displaystyle \alpha \simeq 13^o`

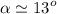
Rounding the magnitude

`\displaystyle \left | \vec{u}+\bar{v} \right |\simeq 23`