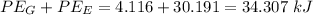Question

A 70.0 kg stuntman is attached to a bungee cord with an unstretched length of 15.0 m. He jumps off a bridge spanning a river from a height of 50.0 m. When he finally stops, the cord has a stretched length of 44.0 m. Treat the stuntman as a point mass, and disregard the weight of the bungee cord. Assuming the spring constant of the bungee cord is 71.8 N/m, what is the total potential energy relative to the water when the man stops falling?

Answer 1

The total potential energy is 34.307 kJ

Solution:

As per the question:

Mass of the stuntman, m = 70.0 kg

Length of the unstretched cord, l = 15.0 m

Height of the cord, H = 50.0 m

The stretched length of the cord,
`\Delta l = 44.0\ m`

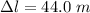
Spring constant of the cord, k = 71.8 N/m

Now,

The total potential energy is given as the sum of gravitational potential energy and elastic potential energy:

The height attained, h = H -
`\Delta l` = 50.0 - 44.0 = 6.0 m

PE_{G} = mgh =
`70* 9.8* 6.0 = 4116\ J = 4.116\ kJ`

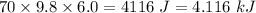
Now, the elastic potential energy:

x = l -
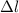`\Delta l` = 44.0 - 15.0 = 29.0 m

`PE_(E) = (1)/(2)kx^(2) = (1)/(2)* 71.8* (29)^(2) = 30.191\ kJ`

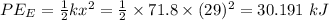
The Total Potential Energy:

`PE_(G) + PE_(E) = 4.116 + 30.191 = 34.307\ kJ`