Answer:
Value of y = 7
Explanation:
By the midpoint theorem of the triangles,
"Segment joining midpoints of the two sides of a triangle is parallel to the third side and measure half the length of the third side."
Therefore, from the figure attached,
In ΔFGH,
J and K are the mid points of the two sides GH and FH.
By theorem, segment JK║GF and m(JK) =
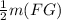
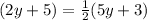
(5y + 3) = 2(2y + 5)
5y + 3 = 4y + 10
5y - 4y = 10 - 3
y = 7