Question

A 300-kg object and a 600-kg object are separated by 4.60 m.

(a) Find the magnitude of the net gravitational force exerted by these objects on a 35.0-kg object placed midway between them. N
(b) At what position (other than an infinitely remote one) can the 35.0-kg object be placed so as to experience a net force of zero from the other two objects

Answer 1

Step-by-step explanation:

m1 = 300 kg

m2 = 600 kg

d = 4.6 m

(a) m = 35 kg

Let the force between m1 and m is F1. Use the Newton's gravitation law

`F_(1)=(Gm_(1)m)/(\left (0.5d  \right )^(2))`

`F_(1)=(6.67* 10^(-11)* 300* 35)/(2.3* 2.3)`

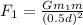
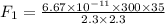
F1 = 1.324 x 10^-7 N (towards m1, i.e., leftwards)

Let the force between m2 and m is F2. Use the Newton's gravitation law

`F_(1)=(Gm_(2)m)/(\left (0.5d  \right )^(2))`

`F_(1)=(6.67* 10^(-11)* 600* 35)/(2.3* 2.3)`

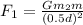
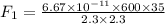
F1 = 2.65 x 10^-7 N (towards m2, i.e., rightwards)

Net force on m is

F = F2 - F1

F = (2.65 - 1.324) x 10^-7

F = 1.33 x 10^-7 N towards right

(b) Let it is placed at a distance r from m1 so that the net force is zero.

`(Gm_(1)m)/(r^(2))=(Gm_(2)m)/(\left ( d-r \right )^(2))`

`(300)/(r^(2))=(600)/(\left ( d-r \right )^(2))`

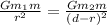
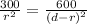
1.414 r = 4.6 - r

2.4 r = 4.6

r = 1.92 m

Thus, the net force on 35 kg is zero at a distance of 1.92 m from 300 kg.

Answer 2

`1.32391* 10^(-7)\ N`

2.69 m

Step-by-step explanation:

M = Mass in the middle = 35 kg

`m_1` = 600 kg

`m_2` = 300 kg

r = Distance

The net force between the objects would be

`F=(GMm_1)/(r^2)-(GMm_2)/(r^2)\\\Rightarrow F=(GM(m_1-m_2))/(r^2)\\\Rightarrow F=(6.67* 10^(-11)* 35(600-300))/(2.3^2)\\\Rightarrow F=1.32391* 10^(-7)\ N`

The magnitude of the net gravitational force exerted by these objects is
`1.32391* 10^(-7)\ N`

Now,

`(GMm_1)/(r^2)=(GMm_2)/((4.6-r)^2)\\\Rightarrow (m_1)/(r^2)=(m_2)/((4.6-r)^2)\\\Rightarrow r^2-9.2r+21.16=(m_2)/(m_1)r^2\\\Rightarrow r^2-9.2r+21.16=(300)/(600)r^2\\\Rightarrow r^2-9.2r+21.16=0.5r^2\\\Rightarrow 0.5r^2-9.2r+21.16=0\\\Rightarrow 50r^2-920r+2116=0`

Solving the above equation we get

`r=(-\left(-920\right)+√(\left(-920\right)^2-4\cdot \:50\cdot \:2116))/(2\cdot \:50), (-\left(-920\right)-√(\left(-920\right)^2-4\cdot \:50\cdot \:2116))/(2\cdot \:50)\\\Rightarrow r=15.7, 2.69`

So, the distance at which the force will ben zero is 2.69 m