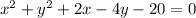Question

Write the equation of the circle in standard form if the points (3,5) and (-5,-1) are endpoints of the diameter

Answer 1

The equation of the circle in standard form if the points (3,5) and (-5,-1) are endpoints of the diameter is

`x^(2)+y^(2) +2x-4y-20=0`

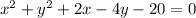
Explanation:

Let AB be the Diameter and the end points be

point A( x₁ , y₁) ≡ ( 3 , 5)

point B( x₂ , y₂) ≡ (-5 , -1)

A circle is given as AB is a Diameter.

To Find:

Equation of the circle in standard form = ?

Solution:

Diameter form of the equation of the circle is

(x - x₁)(x - x₂) + (y - y₁)(y - y₂ ) = 0

Where ( x₁ , y₁) and ( x₂ , y₂) are the endpoints of the diameter.

So on substituting the value we get the required equation of circle

(x - 3)(x - (-5)) + (y - 5)(y - (-1)) = 0

∴ (x - 3)(x + 5) + (y - 5)(y + 1) = 0

Applying Distributive property we get

`x(x+5)-3(x+5)+y(y+1)-5(y+1)=0\\\\x^(2)+5x-3x-15+y^(2)+y-5y-5=0\\x^(2)+y^(2) +2x-4y-20=0\\\therefore x^(2)+y^(2) +2x-4y-20=0\ \textrm{which is the required equation of the circle}`

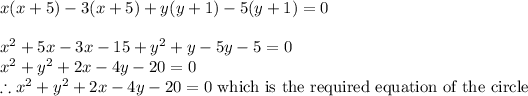
The equation of the circle in standard form if the points (3,5) and (-5,-1) are endpoints of the diameter is

`x^(2)+y^(2) +2x-4y-20=0`