Question

Triangle ABC was dilated by 50%. What is the relationship between AC and A'C'?

Answer 1

D) 1 /2 (AC) = A'C'

Explanation:

The solution is 1 /2 AC = A'C'. The side lengths in ΔABC are twice the side lengths in ΔA'B'C'.

Answer 2

The length of segment AC is two times the length of segment A'C'

Explanation:

we know that

If two figures are similar, then the ratio of its corresponding sides is proportional and this ratio is called the scale factor

Let

z ----> the scale factor

A'C' ----> the length of segment A'C'

AC ----> the length of segment AC

so

`z=(A'C')/(AC)`

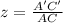
we have that

`z=50\%=50/100=(1)/(2)` ---> the dilation is a reduction, because the scale factor is less than 1 and greater than zero

substitute

`(1)/(2)=(A'C')/(AC)`

`AC=2A'C'`

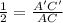
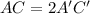
therefore

The length of segment AC is two times the length of segment A'C'