Question

In 2017, the average credit score for loans that were purchased by a government-sponsored mortgage loan company was 744. A random sample of 35 mortgages recently purchased by the company was selected, and it was found that the average credit score was 753 with a sample standard deviation of 19. Complete parts a through c.

a. Using a = 0.05, is there enough evidence from this sample to conclude that the average credit score for mortgages purchased by the company has increased since 2017?
Determine the null and alternative hypotheses. Hos 744 H: > 744 (Type integers or decimals. Do not round.) Determine the appropriate critical value. Select the correct choice below and fill in the answer box within your choice. (Round to three decimal places as needed.)
A. -ta= ________
B. tą = 1.691
C. ta/2=___________-

b. Determine the precise p-value for this test using Excel. The p-value is 0.004
The p-value is 0.004 (Round to three decimal places as needed.)

c. What assumptions need to be made to perform this analysis? Select all that apply.
A. The population is normally distributed.
B. The sample mean is large.
C. No assumptions are necessary.
D. The sample is large.
E. The population standard deviation is small.

Answer 1

The null hypothesis is that the average credit score for mortgages purchased by the company has not increased since 2017, while the alternative hypothesis is that it has increased. The appropriate critical value for a right-tailed test at a significance level of 0.05 is 1.691. The precise p-value for this test is 0.004, which is less than 0.05, so we reject the null hypothesis and conclude that there is enough evidence to suggest an increase in the average credit score.

Step-by-step explanation:

Null and Alternative Hypotheses

The null hypothesis (H0) is that the average credit score for mortgages purchased by the company has not increased since 2017, which is 744. The alternative hypothesis (Ha) is that the average credit score for mortgages purchased by the company has increased since 2017, which is greater than 744.

Critical Value

The appropriate critical value for a right-tailed test with a significance level (α) of 0.05 is t0.05, df=34 = 1.691.

P-Value

The precise p-value for this test, calculated using Excel, is 0.004. Since the p-value is less than 0.05, we reject the null hypothesis and conclude that there is enough evidence from this sample to conclude that the average credit score for mortgages purchased by the company has increased since 2017.

Assumptions

The assumptions that need to be made to perform this analysis are: A. The population is normally distributed and E. The population standard deviation is small.

Answer 2

a) Null hypothesis:
`\mu \leq 744`

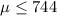
Alternative hypothesis:
`\mu > 744`

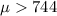
B.
`t_(\alpha)=1.691`.

b)
`p_v = P(t_(34) >2.802)=0.004`

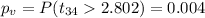
And the code in excel to find it is given by:"=1-T.DIST(2.802,34,TRUE)"

c) A. The population is normally distributed.

D. The sample is large.

Step-by-step explanation:

Part a

We need to conduct a hypothesis in order to determine if actual mean is higher than 744 , the system of hypothesis would be:

Null hypothesis:
`\mu \leq 744`

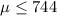
Alternative hypothesis:
`\mu > 744`

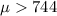
We don't know the population deviation, so for this case is better apply a t test to compare the actual mean to the reference value, and the statistic is given by:

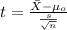`t=(\bar X-\mu_o)/((s)/(√(n)))` (1)

In order to find the critical value, first we need to determine the degrees of freedom given by:

`df=n-1=35-1=34`

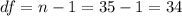
And now since is a right tailed test we need a quantile from the t distribution with 34 degrees of freedom that accumulates 0.05 of the are on the right and 0.95 of the area on the left. We can use the following excel code to find it: "=T.INV(0.95,34)" and we got that
`t_(\alpha)=1.691`.

Part b

Calculate the statistic

We can replace in formula (1) the info given like this:

`t=(753-744)/((19)/(√(35)))=2.802`

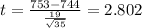
And in order to calculate the p value we can do this, since it's a right tailed test:

`p_v = P(t_(34) >2.802)=0.004`

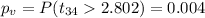
And the code in excel to find it is given by:"=1-T.DIST(2.802,34,TRUE)"

Conclusion

Since our calculated value it's higher than the critical value we have enough evidence at 5% of significance to reject the null hypothesis.

Part c

The 5 assumptions in order to conduct a t test are:

1) The scale of measurement of the data needs to be continuous or ordinal scale

2) We need data from simple random sample sampling, in order to be representative.

3) We need data from a normal distribution, that's called normality assumption.

4) We need a large sample size.

5) And we need homogeneity of variance on the measurements.

Based on this the best options for this case are:

A. The population is normally distributed.

D. The sample is large.