Answer:
Approximately
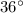 , assuming that the tree is upright.
, assuming that the tree is upright.
Explanation:
Refer to the diagram attached. The upright tree and its shadow are in a right triangle. In this right triangle, the angle of elevation of the sun would be the angle adjacent to the shadow of this tree. At the same time, this angle would be opposite to the side representing the tree. Thus, the tangent of this angle could be represented as:
 .
.
Take the arctangent of this value to find the measure of this angle:
 .
.
Thus, the angle of elevation of the sun at this moment would be approximately
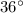 .
.