Question

Find the x-intercept for y = 3x^2 + 6x − 10

Answer 1

x-intercepts: (-3.08, 0) and (1.08, 0)

Explanation:

Given:

The function is given as:

`y=3x^2+6x-10`

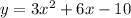
In order to find the x-intercept, we need to equate the given function to 0 as x-intercept is the point where the 'y' value is 0. So,

`y=0\\3x^2+6x-10=0`

Now, this is a quadratic equation of the form
`ax^2+bx+c=0`

We find the solution using the quadratic formula,

`x=(-b\pm √(b^2-4ac))/(2a)`

Here,
`a=3,b=6,c=-10`

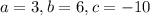
Now, the solutions are:

`x=(-6\pm √(6^2-4(3)(-10)))/(2(3))\\\\x=(-6\pm √(36+120))/(6)\\\\x=(-6\pm √(156))/(6)\\\\x=(-6)/(6)-(2√(39))/(6)\ or\ x=(-6)/(6)+(2√(39))/(6)\\\\x=-1-2.08\ or\ x=-1+2.08\\\\x=-3.08\ or\ x=1.08`

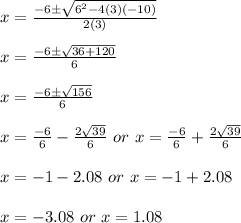
Therefore, the x-intercepts are (-3.08, 0) and (1.08, 0)