Question

Question 11

Find the value of x when lines w and v are parallel.

A 15.5
B 17
C 23.25
D 29.5

Answer 1

The value of x for the given transversal line t and parallel lines w , v is 17

Explanation:

Given as :

The two parallel lines are w and v

The tow parallel lines are transversal intersecting by another line t at two points as show

Let The angle made by transversal when intersecting the line w is ∠a

And The angle made by transversal when intersecting the line v is ∠b

∵ line w ║ line v

∴ ∠a = ∠b ( corresponding lines axiom )

So, from figure

(4 x - 3)° = 65°

Or, 4 x = 65° + 3°

Or, 4 x = 68°

∴ x =
`(68^(\circ))/(4^(\circ))`

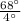
I.e x = 17

So, The value of x = 17

Hence The value of x for the given transversal line t and parallel lines w , v is 17 . Answer