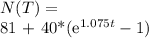Answer:
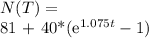
Explanation:
This problem can be solved by the logistic equation of populations, that is:
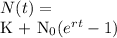
In which K is the carrying capacity of the population,
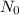 is the initial population, r is the decimal growth rate and t is the period of time.
is the initial population, r is the decimal growth rate and t is the period of time.
In this problem, we have that:
When t = 0, the population is 40: This means that
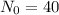 .
.
The manager of a national park determines that the park can sustain 81 coyotes. This means that
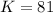 .
.
When t = 1, the population has increased to 60. This means that
 .
.
To write the equation, we have to find the value of r.
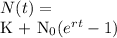
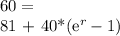
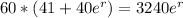
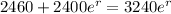
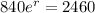
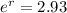
Now we apply ln to both sides, and:
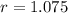
The answer is: