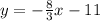Question

Write equation for (-6,5) and (-3,-3)

Answer 1

`y=-(8)/(3)x-11`

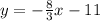
Explanation:

Given:

Two points on a line are given as:

(-6, 5) and (-3, -3)

Now, equation of a line with two points
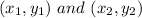`(x_1,y_1)\ and\ (x_2,y_2)` is given as:

`y-y_1=m(x-x_1)`

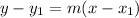
Where, 'm' is the slope and is given as:

`m=(y_2-y_1)/(x_2-x_1)`

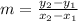
Now, plugging the value of 'm' in the above equation, we get:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

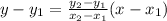
Here,
`(x_1,y_1)=(-6,5)\ and\ (x_2,y_2)=(-3,-3)`

`y-5=((-3-5)/(-3-(-6)))(x-(-6))\\\\y-5=((-8)/(-3+6))(x+6)\\\\y-5=(-8)/(3)(x+6)\\\\y-5=-(8)/(3)x-16\\\\y=-(8)/(3)x-16+5\\\\y=-(8)/(3)x-11`

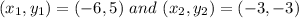
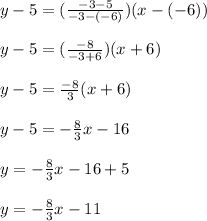
Therefore, the equation of a line passing through (-6,5) and (-3,-3) is:

`y=-(8)/(3)x-11`