Question

A researcher takes a simple random sample of 83 homes in a city and finds that the mean square footage is 1628 with a standard deviation of 243 square feet. What is the 90% confidence interval for the mean square footage of all the homes in that city?

Answer 1

Answer: The correct answer is: (1584 ft2, 1672 ft2).

Explanation:

I hope this helps! :)

Answer 2

Answer: (1583.63, 1672.37)

Explanation:

Given : Sample size : n= 83

Sample mean :
`\overline{x}=1628`

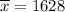
Sample standard deviation :
`\sigma=243`

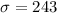
The population standard deviation
`(\sigma)` is unknown .

The confidence interval for population mean :

`\overline{x}\pm t_(\alpha/2)(s)/(√(n))`

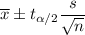
For 90% confidence , significance level =
`\alpha=1-0.90=0.10`

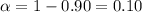
Using t-distribution table , Critical t-value =
`t_((\alpha/2, n-1))=t_(0.05,82)=1.6636`

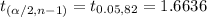
, where n-1 is the degree of freedom.

Now , 90% confidence interval for the mean square footage of all the homes in that city will be :-

`1628\pm (1.6636)(243)/(√(83))\\\\ 1628\pm (1.6636)(26.672715)\\\\\\\\\approx1628\pm 44.37\\\\=(1628- 44.37,\ 1628+ 44.37)\\\\=(1583.63,\ 1672.37)`

Hence, the 90% confidence interval for the mean square footage of all the homes in that city = (1583.63, 1672.37)