Question

Please help!!

1.The height of a projectile is a function of the time it is in the air. The height in feet for t seconds is given by the function h(t) = -16t2 + 96t . What is the domain of the function? What does the domain mean in the context of the problem?

2.Use the graph at right to answer the following question.


Solve for f(x) = -3

Answer 1

Problem 1

The domain is
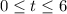`0 \le t \le 6` which in interval notation is [0, 6]

This is the set of t values where h(t) is positive or zero. Any other t values will make h(t) to be negative. So we ignore those t values. A negative height makes no sense.

The domain in the context of the problem means that the projectile is in the air from the time markers of t = 0 and t = 6. In short, the object is in the air for 6 seconds. It takes 6 seconds for it to hit the ground.

Here's how we can determine those t values. We plug in h(t) = 0 and solve for t.

h(t) = -16t^2 + 96t

-16t^2 + 96t = 0

-16t(t - 6) = 0

-16t = 0 or t - 6 = 0

t = 0/(-16) or t = 6

t = 0 or t = 6

======================================================

Problem 2

Draw a horizontal line through -3 on the y axis.

This horizontal line touches the blue graph at the points (-2,-3) and (2,3)

This means the inputs x = -2 and x = 2 lead to the output of y = -3

Therefore f(-2) = -3 and f(2) = -3

Answer: The solutions are x = -2 and x = 2