Question

A manufacturer produces piston rings for an automobile engine. It is known that ring diameter is normally distributed with σ=0.001 millimeters. A random sample of 15 rings has a mean diameter of x¯=74.021. Construct a 99% two-sided confidence interval on the true mean piston diameter and a 95% lower confidence bound on the true mean piston diameter. Round your answers to 3 decimal places.

Answer 1

Answer with explanation:

The confidence interval for population mean is given by :-

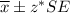`\overline{x}\pm z^* SE` (1)

, where
`\overline{x}` = sample mean

z* = critical value.

SE = standard error

and
`SE=(\sigma)/(√(n))` ,
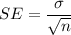`\sigma` = population standard deviation.

n= sample size.

As per given , we have

`\overline{x}=74.021`

`\sigma=0.001`

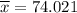
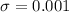
n= 15

It is known that ring diameter is normally distributed.

`SE=(0.001)/(√(15))=0.000258198889747\approx0.000258199`

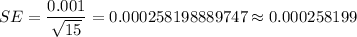
By z-table ,

The critical value for 95% confidence = z*= 1.96

A 99% two-sided confidence interval on the true mean piston diameter :

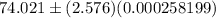`74.021\pm (2.576) (0.000258199)` (using (1))

`74.021\pm 0.000665120624`

`74.021\pm 0.000665120624\\\\=(74.021- 0.000665120624,\ 74.021+ 0.000665120624)\\\\=(74.0203348794,\ 74.0216651206)\approx(74.020,\ 74.022)` [Rounded to three decimal places]

∴ A 99% two-sided confidence interval on the true mean piston diameter = (74.020, 74.022)

By z-table ,

The critical value for 95% confidence = z*= 1.96

A 95% lower confidence bound on the true mean piston diameter:

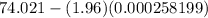`74.021- (1.96) (0.000258199)` (using (1))

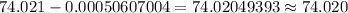`74.021- 0.00050607004=74.02049393\approx74.020` [Rounded to three decimal places]

∴ A 95% lower confidence bound on the true mean piston diameter= 74.020