Question

The following is the balanced equation of the combustion of methane gas with oxygen gas:

CH4(g) + 2O2(g) -> CO2(g) + 2H2O(l)
If you ran a reaction in a sealed balloon at 25o C with 1 g of methane, CH4, and 3 g of oxygen, O2, what is the end volume of the balloon once the reaction is complete? The pressure was constant at 1 atm. Assume all gases behave ideally and you have 100% yield. (ignore vapor pressure of water)

A. 4.9 L
B. 0.096 L
C. 1.1 L
D 1.5 L
E. 0.13 L

Answer 1

The correct option is: C. 1.1 L

Step-by-step explanation:

Given: Temperature: T = 25°C = 25 +273 = 298K (∵ 1°C = 273K)

Pressure: P = 1 atm, Given mass of- CH₄: m₁ = 1g; O₂: m₂ = 3g

Volume: V= ?

Molar mass of CH₄: M₁ = 16g; O₂: M₂ = 32g

As Number of moles:
`n = (given\: mass (m))/(molar\: mass (M))`

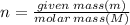
∴ Number of moles of CH₄:
`n_(1) = (m_(1))/(M_(1)) = (1 g)/(16 g) = 0.0625 mol`

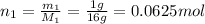
Number of moles of O₂:
`n_(2) =\frac {m_(2)}{M_(2)} = (3 g)/(32 g) = 0.0937 mol`

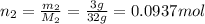
In the given reaction: CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O(l)

1 mole of methane (CH₄) reacts with 2 moles oxygen (O₂) to give 1 mole of CO₂.

So 0.0625 mol of CH₄ reacts with
`(2 * 0.0625)/(1) = 0.125 mol \: O_(2)`.

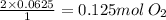Thus the limiting reagent is O₂.

Now, 2 moles O₂ gives 1 mole of CO₂

So 0.0937 mol O₂ gives
`(1 * 0.0937)/(2) = 0.0468 mol \:CO_(2)`

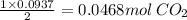
Therefore, the total number of moles of gas after the completion of the reaction: n = number of moles of CO₂: n₃ = 0.0468 mol

Now to calculate the volume of the balloon, we use the ideal gas law:
`PV =nRT`

`\Rightarrow V = (nRT)/(P)`

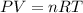
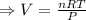
Here, R is the gas constant = 0.08206 L·atm/(mol·K)

T is Temperature,

P is Pressure,

n is Total number of moles of gas

and, V is Volume

Therefore, the volume of the balloon after the completion of the reaction:

`V = (n_(3)RT)/(P)`

`V = (0.0468 mol * 0.08206 L.atm/(mol.K) * 298K)/( 1atm)`

`\Rightarrow V = 1.14 L`

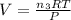
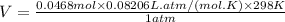
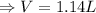
Therefore, the total volume of the balloon after the completion of the reaction: V = 1.14 L