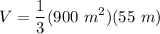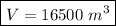1 Answer

Idontgetoutmuch · Answer 1 · 2020-08-07T17:59:23+0000

Answer:

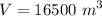
$\displaystyle V=16500\ m^3$

Explanation:

Volume Of A Pyramid

The volume of a pyramid is computed as one third of the product of the area of the base (B) by the height (H):

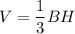
$\displaystyle V=(1)/(3)BH$

The question doesn't ask for anything in particular, so I'm computing the volume of the solid shown in the image

We have a rectangular base of dimensions 15m x 60 m. The area of the base is

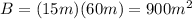
B=(15m)(60m)=900m^2

We now calculate the volume, knowing the height is 55 m

$\displaystyle V=(1)/(3)(900\ m^2)(55\ m)$

$\boxed{\displaystyle V=16500\ m^3}$

Please log in or register to add a comment.