Question

The rectangle below has an area ofy4+11y2+30y 4 +11y 2 +30y, start superscript, 4, end superscript, plus, 11, y, squared, plus, 30 square meters and a length ofy2+5y 2 +5y, squared, plus, 5 meters.What expression represents the width of the rectangle

Answer 1

The width of the rectangle is
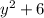`y^2+6` meters.

Explanation:

Given :

Area of Rectangle =
`y^4+11y^2+30 \ m^2`

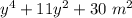
Length of Rectangle =
`y^2+5\ meters`

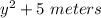
We need to find the width of the rectangle.

Now We know that area of rectangle can be calculated by multiplying length and width.

Area of Rectangle =
`length * width`

Hence Width can be calculated as;

Width of rectangle =
`\frac{\textrm{Area of Rectangle}}{Length}`

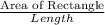
Now Substituting the values we get;

Width of rectangle =
`(y^4+11y^2+30)/(y^2+5)`

Now by performing long division we will find the width of rectangle;

Long Division is performed in attachment;

Explanation of Long Division is Given below;

Step 1 : we have dividend
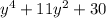`y^4+11y^2+30` and divisor
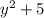`y^2+5` we will first multiply with
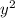`y^2` so the Quotient is
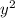`y^2` and Remainder is
`6y^2+30`

Step 2: Now we have dividend
`6y^2+30` and divisor
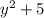`y^2+5` we will fmultiply with
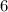`6` so the Quotient is
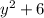`y^2+6` and Remainder is 0.

Hence The width of the rectangle is
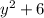`y^2+6` meters.