Answer:
The True statement for a line TU is
Line TU is parallel to line RS
Step-by-step explanation:
Given:
Let,
point R( x₁ , y₁) ≡ ( -5, 3)
point S( x₂ , y₂) ≡ (5 , 1)
and
point T( x₁ , y₁) ≡ ( -1, -2)
point U( x₂ , y₂) ≡ (4 , -3)
We have Line RS and Line TU
Slope of any Line having Two points ( x₁ , y₁) and ( x₂ , y₂) Given by
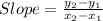
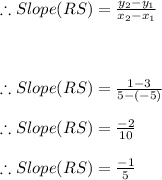
Similarly,
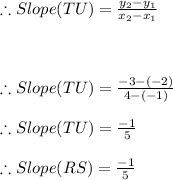
Now,
Slope of RS = Slope of TU
We Know, if the slopes are equal then the lines are parallel.
Therefore line TU is parallel to line RS is the true statement about line TU.